離散フーリエ変換によるヘクサコード定理の証明
$$ \gdef\Z#1{\mathbb{Z}_{#1}} $$
概要
ピッチクラス ・セット理論の古典的な定理「ヘクサコード定理（Hexachordal theorem）」の証明です．
証明の流れは Music Through Fourier Space の第一章を参考にさせていただきました[1]． link.springer.com
ヘクサコード定理の証明を通じて，ピッチクラス・セットの離散フーリエ変換における基礎事項を整理することも兼ねています．
- 概要
- 背景
- 証明の流れ
- 表記の注意
- ピッチクラス
- ピッチクラス・セット
- 移置（Transposition）と転回（Inversion）
- specific音程
- IFunc（Inerval Function）
- IC（Interval Content）
- Homometric
- ヘクサコード定理
- PCセットのDistribution
- 離散フーリエ変換
- 逆離散フーリエ変換
- 畳み込み定理
- 基礎的な事実
- ルーウィンの補題
- ヘクサコード定理の証明
- 最後に
- 参考文献
背景
アメリカの音楽理論家／作曲家であるミルトン・バビット（1916-2011），デイヴィッド・ルーウィン（1933-2003）らによって1950年代に発見されたヘクサコード定理（Hexachordal theorem）は，6音のピッチクラス ・セットの性質に関する有名な定理です[2]．元は 12平均律で示されましたが， 離散フーリエ変換 と呼ばれる数学的道具を用いると，一般の偶数平均律で成り立つことを証明できます．
ところで音楽とフーリエ変換といえば，音声信号の周波数分析を思い浮かべる方も多いかもしれませんが，ここではそれを扱いません．代わりに，抽象的な対象である「ピッチクラス・セット 」に対する離散フーリエ変換を考えます．
証明の流れ
まずはヘクサコード定理を説明するために必要な概念を定義します．そしてピッチクラス・セットにおける離散フーリエ変換のアイデアを説明し，ルーウィンの補題と呼ばれる重要な定理を証明します．
最後に，ルーウィンの補題を用いてヘクサコード定理を証明します．
表記の注意
- $\Z{n}$ は，$0$ から $n-1$ までの整数を要素として持つ，位数 $n$ の巡回群 $\mathbb{Z} / n \mathbb{Z}$ の略記です．
- $\Z{n}$ 上の演算では，剰余をとる記号 ${} \mod {}$ を暗黙に省略する場合があります（例： $b - a \equiv k \pmod n$ を単に $b - a = k$ と書く）．
ピッチクラス
西洋音楽のピッチ表記法において，オクターブまたは異名同音の関係にあるピッチの集まりを ピッチクラス （Pitch-class）と呼びます．
同一音名でオクターブが異なるピッチは，同じピッチクラス に属する $$ 0 = \Set{ \ldots C_0, C_1, C_2, C_3, C_4, C_5, C_6, \ldots } $$
異名同音の関係にあるピッチは，同じピッチクラス に属する $$ 3 = \Set{ \ldots D\char"266f, E\char"266d, F\char"1d12b \ldots } $$
一般に $n$平均律 $(n \in \mathbb{N}^{+})$ には $n$個のピッチクラス が存在し，$0$ から $n{-}1$ の数と対応付けて表記します．
12平均律のピッチクラス
| 音名 | ピッチクラス | 音名 | ピッチクラス | 音名 | ピッチクラス |
|---|---|---|---|---|---|
| C | 0 | E | 4 | G♯／A♭ | 8 |
| C♯／D♭ | 1 | F | 5 | A | 9 |
| D | 2 | F♯／G♭ | 6 | A♯／B♭ | 10 |
| D#／E♭ | 3 | G | 7 | B | 11 |
ピッチクラス・セット
ピッチクラスの集合をピッチクラス ・セット（Pitch-class set）と呼びます．しばしば省略してPCセット（PC-set）と書かれます．
12平均律のピッチクラス・セットの例
Cメジャーコード（C, E, G）：$\Set{ 0, 4, 7 }$
Cメジャースケール（C, D, E, F, G, A, B）：$\Set{ 0, 2, 4, 5, 7, 9, 11 }$
集合なので順序や重複度は考えず，単に和音や音階の内容のみを表します．
移置（Transposition）と転回（Inversion）
ピッチクラス・セット理論における，2つの基本的な操作を定義します．
移置（Transposition）
ある PCセット $A \in \Z{n}$ の $p$ による Transposition とは，以下の写像による像である．
$$
T_p(A) = \Set{a + p \pmod n | a \in A}
$$
転回（Inversion）
ある PCセット $A \in \Z{n}$ の $p$ による 転回とは，以下の写像による像である．
$$
I_p(A) = \Set{- a + p \pmod n | a \in A}
$$
Gメジャーコードの 5 による 移置
Gメジャーコード $\Set{7, 11, 2}$ の各要素を $+5$ すればよいので,
$$
7 + 5 \equiv 0 \pmod {12} \\
11 + 5 \equiv 4 \pmod {12} \\
2 + 5 \equiv 7 \pmod {12} \\
$$
より，Cメジャーコード $\Set{0, 4, 7}$．
移置は，平均律のグリッドに沿ってそのまま全体を平行移動させるイメージです．
Gメジャーコードの 2 による 転回
Gメジャーコード $\Set{7, 11, 2}$ の各要素に $-1$ を掛けて $+2$ すればよいので,
$$
-7 + 2 \equiv 7 \pmod {12} \\
-11 + 2 \equiv 3 \pmod {12} \\
-2 + 2 \equiv 0 \pmod {12} \\
$$
より，Cマイナーコード $\Set{0, 3, 7}$．
転回は，ある選んだ軸を対象に鏡像反転させるイメージです．
specific音程
2つのピッチクラス間の，オクターブ差を無視した音程に相当する概念を導入します．
specific音程
n平均律の ある2つのピッチクラス $a$ から $b$ への specific音程（specific interval）とは，次の関数$\text{int}$で定義される $0$ から $n{-}1$ の整数である．
$$
\text{int}(a, b) = b - a \pmod n
$$
12平均律における G から E への specific音程
E(ピッチクラス 4) から G(ピッチクラス 7) を引けば良いので，
$$
\text{int}(7, 4) = 4 - 7 = -3 \equiv 9 \pmod {12}
$$
よって，specific音程は 9．
IFunc（Inerval Function）
2つのPCセット$A, B \in \Z{n}$ の間には，様々なspecific音程の組み合わせが存在しますが，これらを全て数えてヒストグラムを与える関数を考えます． これはつまり，2つのPCセット間の"音程"のようなイメージです．
IFunc
$$
\begin{equation*}
\begin{split}
& \text{IFunc}(A, B)(k) = \\
& \quad \# \Set{ (a, b) \in A \times B | b - a \equiv k (\operatorname{mod} n) } \\
\end{split}
\end{equation*}
$$
$\#$ は集合の元の個数を表す記号です．
IFuncは，PCセット $A, B$の全てのペア(直積集合)の中から，「$a$ から $b$ への specific音程が $k$ であるもの」の総数を求めることを意味しています．
IFunc の計算例
12平均律で，$A = \Set{0,4,7}$，$B = \Set{5,9}$ の場合を考える． $A$ と $B$ のペアは，
$$
A \times B = \Set{(0,5), (4,5), (7,5), (0,9), (4,9), (7,9)}
$$
の6種類であり，それぞれの specific音程を求めると，
$$
\text{int}(0,5) = 5 - 0 \equiv 5 \\
\text{int}(4,5) = 5 - 4 \equiv 1 \\
\text{int}(7,5) = 5 - 7 \equiv 10 \\
\text{int}(0,9) = 9 - 0 \equiv 9 \\
\text{int}(4,9) = 9 - 4 \equiv 5 \\
\text{int}(7,9) = 9 - 7 \equiv 2 \\
$$
となる．ここで例えば $\text{IFunc}(A, B)(5)$ とは，上記の中に「specific音程 $5$ であるものが」何個あるか数えることを意味するので，
$$
\text{IFunc}(A, B)(5) = 2
$$
となる．なお，$\text{IFunc}(A, B)(0)$ から $\text{IFunc}(A, B)(11)$ までの計算結果を並べると，
$$
\text{IFunc}(A, B) = \lbrack 0,1,1,0,0,2,0,0,0,1,1,0 \rbrack
$$
IC（Interval Content）
IFunc と同様の考え方で，今度は 1つの PCセット $A \in \Z{n}$ の内部にある specific音程 のヒストグラムを与える関数を考えます．
IC（Interval Content）
$$
\text{IC}_A(k) = \# \Set{ (i, j) \in A^{2} | i - j = k}
$$
または，IFunc を用いて，
$$
\text{IC}_A(k) = \text{IFunc}(A, A)(k)
$$
ICの計算例
12平均律で，$A = \Set{0,4,7}$，の場合を考える． $A$ と $A$ のペアは，
$$
A \times A = \Set{(0,0), (0,4), (0,7), (4,0), (4,4), (4,7), (7,0), (7,4), (7,7)}
$$
の9種類であり，それぞれの specific音程を求めると，
$$
\text{int}(0,0) = 0 - 0 \equiv 0 \\
\text{int}(0,4) = 4 - 0 \equiv 4 \\
\text{int}(0,7) = 7 - 0 \equiv 7 \\
\text{int}(4,0) = 0 - 4 \equiv 8 \\
\text{int}(4,4) = 4 - 4 \equiv 0 \\
\text{int}(4,7) = 7 - 4 \equiv 3 \\
\text{int}(7,0) = 0 - 7 \equiv 5 \\
\text{int}(7,4) = 4 - 7 \equiv 9 \\
\text{int}(7,7) = 7 - 7 \equiv 0 \\
$$
となる．ここで例えば $\text{IC}_A(4)$ とは，上記の中に「specific音程 $4$ であるものが」何個あるか数えることを意味するので，
$$
\text{IC}_A(4) = 1
$$
となる．なお，$\text{IC}_A(0)$ から $\text{IC}_A(11)$ までの計算結果を並べると，
$$
\text{IC}_A = \lbrack 3,0,0,1,1,1,0,1,1,1,0,0 \rbrack
$$
ところで，$\text{IC}_A(0) = 3$ であり $A$の要素数 $3$ と一致していることが観察できる．一般に $\text{IC}_A(0)$ はPCセットの要素数と一致することが知られている．
Interval Content は，ピッチクラス・セット理論において Interval Vector と呼ばれているものに類似する概念です．
Homometric
Interval Content はPCセットごとに様々な値をとりますが，中には同じ値をとる場合が存在します．
この関係には Homometric という名前が付けられています．
Homometric
2つのPCセット $A, B \in \Z{n}$ の $\text{IC}$ が同じ値をとるとき，$A$ と $B$ は Homometric 関係であるという．
特に，$A$ と $B$ が移置と転回によって互いに移せない場合は，特に興味深い Homometric 関係とみなされます．
（一見異なる形状をしている2つのPCセットが，実は同じパーツ（音程）で構成されているというわけです．）
またこれは，ピッチクラス・セット理論において Z-relation と呼ばれている関係とほとんど同じ概念です．
12平均律で最も単純な Homometric 関係
PCセット $A = \Set{0,1,4,6}$ と $B = \Set{0,1,3,7}$ は Homometric 関係で，移置と転回によって互いに移すことができない．
Interval Content は どちらも $\lbrack 4,1,1,1,1,1,2,1,1,1,1,1 \rbrack$ である．
また，これらは4音のPCセットだが，12平均律ではこれより小さい(3音以下)の Homometric 関係は存在しない．
ヘクサコード定理
ヘクサコード (Hexachord) とは，6個のピッチクラスで構成される 12平均律の PCセットを指す用語です．
このヘクサコードにおいては，次のような特別な Homometric 関係が成り立ちます．
ヘクサコード定理
12平均律の 2つのPCセット $A, B \in \Z{12}$ の要素数が $6$（すなわちヘクサコード）のとき，$B$ が $\Z{12}$ における $A$ の補集合ならば，
$A$ と $B$ は同じ Interval Content を持つ（すなわち，Homometricである）．
さらに，この法則は一般の偶数平均律でも成り立つことが知られています．
一般化されたヘクサコード定理
2つのPCセット $A, B \in \Z{2m}$ の要素数が ${m}$ のとき，$B$ が $\Z{2m}$ における $A$ の補集合ならば，
$A$ と $B$ は同じ Interval Content を持つ（すなわち，Homometricである）．
ブルーススケールとその補集合
12平均律で近似した，Cブルーススケール $\Set{0,3,5,6,7,10}$と Aメジャースケールの部分集合 $\Set{1,2,4,8,9,11}$ は，互いに補集合となるヘクサコードで，
Interval Content は どちらも $\lbrack 6,2,3,3,2,4,1,4,2,3,3,2 \rbrack$ である．すなわち Homometric 関係である．
PCセットのDistribution
あるPCセット $A \in \Z{n}$ を一つ選んだとき，その $A$ に依存して $\Z{n}$ の各元 を 複素数体 $\mathbb{C}$ の元へと写す関数 $f_A$ について考えます．
この関数 $f_A$ で $\Z{n}$ の各元 $0, 1, ..., n - 1$ を順番に写していくと，長さ $n$ の複素数列が得られます．
つまり，関数 $f_A$によって PCセット $A$ と 長さ $n$ の複素数列 を対応づける ことができます．
このようにして， 関数 $f_A$ によって構成される列を， $f_A$ による $\Z{n}$ 上の Distribution と呼びます．
そして，具体的な関数 $f_A$ として 特性関数 と呼ばれる関数を用いると，PCセットを $0$ と $1$ で構成される二値数列として表すことができます．
特性関数（Charactaristic function）
集合 $E$ とその部分集合 $A$に対して．$E$ の元 $x$ が $A$ に属する場合は $1$ を，属さない場合は $0$ を返す以下の関数を，
集合$E$ における部分集合 $A$ の特性関数と呼ぶ．
$$
1_A(k) = \begin{cases}
1 &\text{if } k \in A \\\\
0 &\text{if } k \notin A
\end{cases}
$$
ピッチクラス・セットのDistribution
PCセット $A \in \Z{n}$ と，その特性関数 $1\\_A$ によって構成される， $\Z{n}$ 上の Distribution とは，
$\Z{n}$ の 各元 $0, 1, ..., n - 1$ を $1\\_A$ で 写した列 $f$ である．
$$
f = \lbrack 1_A(0), 1_A(1), ... , 1_A(n-1) \rbrack
$$
Cメジャーコード の Distribution
Cメジャーコードに対応するPCセットは $A = \{0, 4, 7\} \in \Z{12}$
特性関数は $$ 1_A(0) = 1 \\ 1_A(4) = 1 \\ 1_A(7) = 1 \\ $$ で，その他は$0$をとるので，Distributionは $$ \Set{ 0, 4, 7 } \xmapsto{1_A} \lbrack 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0 \rbrack $$
特性関数は $$ 1_A(0) = 1 \\ 1_A(4) = 1 \\ 1_A(7) = 1 \\ $$ で，その他は$0$をとるので，Distributionは $$ \Set{ 0, 4, 7 } \xmapsto{1_A} \lbrack 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0 \rbrack $$
離散フーリエ変換
離散フーリエ変換とは，ざっくり言うと時間軸に沿って周期的に繰り返す信号データから，その中にある周期構造をそれぞれの周期毎に分解して取り出す操作で，工学的にも幅広く応用されています．
ところで，PCセットは 「1オクターブ」という周期で繰り返す空間に生息する，信号データのようなもの とみなすことができます．そのように捉えると PCセットに対する離散フーリエ変換 というものを考えることができるようになります．
Distribution の離散フーリエ変換
関数 $f : \Z{n} \mapsto \mathbb{C}$ による Distribution を，別の関数 $\mathcal{F}$ による Distribution へ写す以下の写像を，離散フーリエ変換（Discrete Fourier transform）と呼ぶ．
$$
\mathcal{F}(x) : x \mapsto \sum_{k \in \Z{n}}^{} f(k) \cdot e^{-i2\pi kx/n}
$$
（$e$は自然対数の底，$i$は虚数単位）
PCセットに対する離散フーリエ変換は，PCセット$A$と1対1に対応する特性関数 $1_A$の離散フーリエ変換として定義します．
特性関数の離散フーリエ変換
特に，特性関数 $1_A$ による Distribution に関する離散フーリエ変換は以下の通り．
$$
\begin{equation*}
\begin{split}
\mathcal{F}_A(x) : x \mapsto & \sum_{k \in \Z{n}}^{} 1_{A}(k) \cdot e^{-i2\pi kx/n} \\
= & \sum_{k \in A}^{} e^{-i2\pi kx/n} \\
\end{split}
\end{equation*}
$$
Cディミニッシュ7thコードの離散フーリエ変換
12平均律のPCセット $A = \Set{0,3,6,9}$の特性関数 $1_A$ は，
$$
1_{A} = \lbrack 1,0,0,1,0,0,1,0,0,1,0,0 \rbrack
$$
である．離散フーリエ変換すると，
$$
\begin{equation*}
\begin{split}
\mathcal{F}_A(x) &= \sum_{k \in A}^{} e^{-i2\pi kx/12} \\
&= e^{-i2\pi 0x/12} + e^{-i2\pi 3x/12} + e^{-i2\pi 6x/12} + e^{-i2\pi 9x/12} \\
&= e^0 + (e^{-i \pi /2})^x + (e^{-i \pi})^x + (e^{-i3\pi /2})^x \\
&= 1 + (-i)^x + (-1)^x + i^x \\
&= \begin{cases}
4 &\text{if } x \in \Set{0,4,8} \\
0 &\text{else }
\end{cases} \\
\end{split}
\end{equation*}
$$
したがって，$\mathcal{F}_A = \lbrack 4,0,0,0,4,0,0,0,4,0,0,0 \rbrack $ と計算できる．
ただし，これは離散フーリエ変換の結果が実数となる特殊な場合であり，通常は計算結果が複素数になる．
ただし，これは離散フーリエ変換の結果が実数となる特殊な場合であり，通常は計算結果が複素数になる．
PCセットの離散フーリエ変換の文脈では，特定の周期の値を表す フーリエ係数（Fourier coefficient） という用語がよく使われます．
フーリエ係数
逆離散フーリエ変換
離散フーリエ変換には逆の操作が存在し，一度変換したものを完全に元に戻すことができます．
逆離散フーリエ変換
$$
f(k) = \frac{1}{n} \sum_{k=0}^{N-1} \mathcal{F}(x) \cdot e^{+i2\pi kx/n}
$$
畳み込み定理
2つの関数をずらしながら重ね合わせて，新しい関数を生み出す 畳み込み と呼ばれる操作があります．
畳み込み
$\forall x \in \Z{n}$
$$
(f*g)(x)=\sum_{t \in \Z{n}}^{} {f(t)\,g(x-t)}
$$
また，畳み込みと離散フーリエ変換は深い関係があり，次の定理が成り立つことが知られています．
畳み込み定理
関数 $f$ の離散フーリエ変換を $\widehat{f}$ と表記する．このとき 任意の $x \in \Z{n}$ において，
$$
\widehat{(f*g)}(x) = \widehat{f}(x) \times \widehat{g}(x)
$$
基礎的な事実
以降の証明で使用する，いくつかの基礎的な事実を説明しておきます．
転回された PCセットの表記
ある PCセット $A \in \Z{n}$ の $0$ による 転回 を，単にマイナス記号を付けて表記する．
$$
I_0(A) \iff -A
$$
転回と特性関数の関係
$$
1_A(k) = 1_{-A}(-k \space (\operatorname{mod} n))
$$
証明
転回の定義より，$A$ が $k$ を含む場合に限り，$-A$ は明らかに $-k$ を含む． $\Box$
転回と離散フーリエ変換の関係
PCセット $A$ の転回を離散フーリエ変換することは，$A$ を離散フーリエ変換した複素共役と等しい．
$$
\mathcal{F}_{-A} = \overline{\mathcal{F}_A}
$$
証明
$\mathcal{F}_A$ の複素共役をとって，三角関数の周期性より $\frac{2\pi kx}{n} \mapsto \frac{2\pi kx}{n} - 2\pi x$ へ偏角を置き換える．
$$ \begin{equation*} \begin{split} \overline{\mathcal{F}_A}(x) &= \sum_{k \in \Z{n}}^{} 1_{A}(k) \cdot e^{+i2\pi kx/n} \\ &= \sum_{k \in \Z{n}}^{} 1_{A}(k) \cdot e^{-i2\pi (n-k)x/n} \\ & n-k \equiv -k \pmod n \text{より} \\ &= \sum_{k \in \Z{n}}^{} 1_{A}(k) \cdot e^{-i2\pi (-k)x/n} \\ & 1_{A}(k) = 1_{-A}(-k) \text{より} \\ &= \sum_{k \in \Z{n}}^{} 1_{-A}(-k) \cdot e^{-i2\pi (-k)x/n} \\ & -k = m \text{とおくと} \\ &= \sum_{-m \in \Z{n}}^{} 1_{-A}(m) \cdot e^{-i2\pi mx/n} \\ &= \sum_{m \in A}^{} e^{-i2\pi mx/n} \\ &= \mathcal{F}_{-A}(x) \qquad \Box \\ \end{split} \end{equation*} $$
証明
$$
\begin{equation*}
\begin{split}
\mathcal{F}_A(0) &= \sum_{k \in \Z{n}}^{} 1_{A}(k) \cdot e^{0} \\
&= \sum_{k \in \Z{n}}^{} 1_{A}(k) \\
&= \sum_{k \in A}^{} 1 \\
&= \# A \qquad \Box \\
\end{split}
\end{equation*}
$$
Aggregate の離散フーリエ変換
PCセット $A = \Z{n}$ を Aggregate と呼ぶ（全てのピッチクラス を含む PCセット）．
$x \not = 0$ のとき Aggregate の 離散フーリエ変換 は， $$ \mathcal{F_{\Z{n}}(x)} = 0 $$
$x \not = 0$ のとき Aggregate の 離散フーリエ変換 は， $$ \mathcal{F_{\Z{n}}(x)} = 0 $$
証明
初項 $1$，公比 $e^{-i2\pi x/n}$，長さ $n$ の等比数列の和とみなせる．
$$ \begin{equation*} \begin{split} \mathcal{F_{\Z{n}}(x)} &= \sum_{k \in \Z{n}}^{} e^{-i2\pi kx/n} \\ &= \frac{1 \cdot \lbrace (e^{-i2\pi x/n})^{n} -1 \rbrace}{e^{-i2\pi x/n}-1} \\ &= \frac{e^{-i2\pi x} -1}{e^{-i2\pi x/n}-1} \\ &= \frac{1 -1}{e^{-i2\pi x/n}-1} \\ &= 0 \qquad \qquad \qquad \Box \\ \end{split} \end{equation*} $$
補集合と離散フーリエ変換の関係
$x \not = 0$ のとき，
$$
\mathcal{F}_{\Z{n} \backslash A}(x) = - \mathcal{F}_A(x)
$$
証明
$$
\begin{equation*}
\begin{split}
\mathcal{F}_{\Z{n} \backslash A}(x) &= \sum_{k \in \mathbb{\Z{n} \backslash A}}^{} e^{-i2\pi kx/n} \\
&= \sum_{m \in \Z{n}}^{} e^{-i2\pi mx/n} - \sum_{l \in A}^{} e^{-i2\pi lx/n} \\
&= 0 - \widehat{1_{A}(x)} \\
&= - \mathcal{F}_A(x) \qquad \Box \\
\end{split}
\end{equation*}
$$
ルーウィンの補題
ルーウィンの補題
$\forall k \in \Z{n}$
$$
\widehat{IC_A}(k) = |\mathcal{F}_A(k)|^2
$$
証明 $t \in A$ かつ $t+k \in B$ のとき，$1_A(t) \cdot 1_B(t + k) = 1$ であることに着目すると，$\text{IFunc}$ を以下のように書き換えられる．
$$ \begin{equation*} \begin{split} \text{IFunc}(A, B)(k) &= \# \Set{ (a, b) \in A \times B | b - a \equiv k (\operatorname{mod} n) } \\ &=\sum_{t \in \Z{n}}^{} 1_A(t) \cdot 1_B(t + k) \\ &=\sum_{t \in \Z{n}}^{} 1_{-A}(-t) \cdot 1_B(k-(-t)) \\ & -t = u \text{とおくと} \\ &=\sum_{-u \in \Z{n}}^{} 1_{-A}(u) \cdot 1_B(k-u) \\ &=\sum_{u \in \Z{n}}^{} 1_{-A}(u) \cdot 1_B(k-u) \\ \end{split} \end{equation*} $$
（注：最後の式変型は，$-u$ は $\Z{n}$ における $u$ の逆元より，$u$ が $0$ から $n-1$ を動いて和を取っても同じことなので符号を外している）
畳み込みの定義を思い出すと，これは特性関数 $1_{-A}$ と $1_B$ の畳み込みなので，$\text{IFunc}$ は畳み込みとして表せることが分かる． $$ \text{IFunc}(A, B)(k) = 1_{-A} * 1_B(k) $$
$\text{IFunc}$ の離散フーリエ変換は，畳み込み定理等を用いると， $$ \begin{equation*} \begin{split} \widehat{\text{IFunc}(A, B)} &= \widehat{1_{-A} * 1_B} \\ &= \widehat{1_{-A}} * \widehat{1_{B}} \\ &= \mathcal{F}_{-A} \times \mathcal{F}_B \\ &= \overline{\mathcal{F}_A} \times \mathcal{F}_B \\ \end{split} \end{equation*} $$
以上より，PCセット $A$ における Interval Content の離散フーリエ変換は， $$ \begin{equation*} \begin{split} \widehat{\text{IC}_A} &= \widehat{\text{IFunc}(A, A)} \\ &= \overline{\mathcal{F}_A} \times \mathcal{F}_A \\ &= |\mathcal{F}_A(k)|^2 \qquad \Box \\ \end{split} \end{equation*} $$
ヘクサコード定理の証明
証明
任意のPCセット $A \in \Z{2m}$ と，その補集合 $B = \Z{2m} \backslash A$に対して，$\mathcal{F}_A(x)$ と $\mathcal{F}_B(x)$ を考える．
$x = 0$ の場合
$\mathcal{F}_A(0) = \# A$， $\mathcal{F}_B(0) = \# B$ であり，$\# A = \# B = {m}$ なので，$\mathcal{F}_A(0) = \mathcal{F}_B(0)$．
$x \not = 0$ の場合
ルーウィンの補題より，
$$
\widehat{IC_A} = |\mathcal{F}_A|^2
$$
$\mathcal{F}_{\Z{n} \backslash A} = - \mathcal{F}_A$ なので， $$ \begin{equation*} \begin{split} |\mathcal{F}_A|^2 &= |- \mathcal{F}_{\Z{n} \backslash A}|^2 \\ &= |\mathcal{F}_{\Z{n} \backslash A}|^2 \\ &= \widehat{IC_{\Z{n} \backslash A}} \\ \end{split} \end{equation*} $$
逆離散フーリエ変換より， $$ IC_A = IC_{\Z{n} \backslash A} \qquad \Box $$
最後に
ヘクサコード定理それ自体は興味深いものの，実際の音楽に直接応用できるものではないかもしれません．しかし，証明に使用したPCセットの離散フーリエ変換という道具は，近年活発に研究されている領域でもあります．
- ダイアトニックスケールの一般化の一つである Maximally even sets との関連性 [3]
- フーリエ係数の絶対値と和音の質(Quality)の関連性 [4]
- フーリエ係数の位相と調性(Tonality)の関連性 [5]
- 周期的なリズムへの離散フーリエ変換の応用 [6]
ヘクサコード定理を一通り証明しておくと，基礎的な道具が最低限手に入るので，分野への入門になると期待しています．
参考文献
- Amiot E (2016). Music Through Fourier Space. Springer International Publishing, 1-17. https://doi.org/10.1007/978-3-319-45581-5
- Lewin D (1959). Re: Intervallic Relations between Two Collections of Notes. Journal of Music Theory 3(2), 298–301. https://doi.org/10.2307/842856
- Amiot E. (2007). David Lewin and maximally even sets. Journal of Mathematics and Music, 1(3), 1–21. https://doi.org/10.1080/17459730701654990
- Viaccoz, C., Harasim, D., Moss, F.C., Rohrmeier, M.: Wavescapes: a visual hierarchical analysis of tonality using the discrete Fourier transform. Music Sci. 27(2), 390–427 (2023). https://doi.org/10.1177/10298649211034906
- Yust J (2015b) Schubert’s harmonic language and fourier phase space. J Music Theory 59(1):121–181. https://doi.org/10.1215/00222909-2863409
- Jason Yust, Steve Reich’s Signature Rhythm and an Introduction to Rhythmic Qualities, Music Theory Spectrum, Volume 43, Issue 1, Spring 2021, Pages 74–90, https://doi.org/10.1093/mts/mtaa017
Python + Opycleid でコード進行を分析する（ネオ・リーマン理論）
概要
Python ライブラリの Opycleid を使用して, コード進行からネオ・リーマン理論の変換を表示するプログラムを実装します.
ネオ・リーマン理論とは
1980年代以降, アメリカの研究者らを中心に形作られてきた, 比較的新しい音楽理論です.
一連の研究をゆるく包括する概念のため, 明確に定義するのは難しいですが, コードの機能や進行ではなく, コード間の相対的な変換 (Transformation) に着目する点を特徴としています.
例えば, C → Am というコード進行は, ネオ・リーマン理論的な見方をすると Cに変換Rが作用してAmになる みたいな感じです.
ここでは詳細は割愛させていただき, 参考リンクのみの記載とします.
ネオ・リーマン理論 - Wikipedia
An introduction to neo-Riemannian theory (1)
An introduction to neo-Riemannian theory (6)
ネオ・リーマン理論のリーマン受容にみる概念変容
SoundQuest - ネオ・リーマン理論❶ PLR操作とトネッツ
Opycleid とは
音楽理論研究者の Alexandre Popoff 氏が開発した Python 用のライブラリです.
コードに限らず音楽的オブジェクト(musical object) 一般に対して, オブジェクト間の変換を定義し, 分析することができます.
今回は, その中の一機能を利用して, 24種類の長短三和音の間のネオ・リーマン理論的な分析を行います.
| サイト | URL |
|---|---|
| Github | https://github.com/AlexPof/opycleid |
| 公式ドキュメント | https://alexpof.github.io/opycleid/ |
| チュートリアル | https://alexpof.github.io/opycleid/gettingstarted/ |
(チュートリアルが分かりやすいので, RPL変換と Python の知識がある方はこちらを直接読んでも大丈夫と思います)
環境構築
Python3 と NumPy が動いて Opycleid をインストールできるなら何でも良いのですが, 今回は Google Colaboratory を使用します(Googleアカウントが必要).
なお動作確認時のバージョンは下記の通りです.
Python: 3.10.11
NumPy: 1.22.4
Opycleid: 0.4.2
- ノートブックの新規作成 で, 適当なノートブックを作成します.
!pip install opycleidを実行し, Opycleid をインストールします (Successfully installed opycleid が表示されればOK).
以上で準備完了です. なお, 無料プランでは一定時間でセッションが切断され環境もリセットされるため, その都度 再インストールが必要です.
2つのコード間の変換を求める
「+ コード」をクリックし, 下記を挿入します.
from opycleid.musicmonoids import PRL_Group _monoid = PRL_Group() print(_monoid.get_operation('C_M', 'C_m')) # P print(_monoid.get_operation('C_M', 'A_m')) # R print(_monoid.get_operation('C_M', 'E_m')) # L
実行すると, 各コード間の変換を表す記号が表示されます.
['P'] ['R'] ['L']
上記の例では, opycleid.musicmonoids 名前空間に予め用意されている PRL_Group クラスの get_operation() メソッドを使用して, ネオ・リーマン理論の最も基本的な変換である「P」「R」「L」によってコードがどのように変換されるかを分析しています.
get_operation(変換前のコード名, 変換後のコード名)で, 変換を表す記号のリストを取得できます.
PRLを組み合わせたもっと複雑な変換も分析できます.
print(_monoid.get_operation('C_M', 'Bb_m')) # RLRLP
実行結果：
['RLRLP']
使用可能なコード名の一覧は下記で表示できます（異名同音を無視した24種類）.
for obj in PRL_Group().get_objects(): print(obj[1].get_elements())
実行結果：
['A_M', 'A_m', 'B_M', 'B_m', 'Bb_M', 'Bb_m', 'C_M', 'C_m', 'Cs_M', 'Cs_m', 'D_M', 'D_m', 'E_M', 'E_m', 'Eb_M', 'Eb_m', 'F_M', 'F_m', 'Fs_M', 'Fs_m', 'G_M', 'G_m', 'Gs_M', 'Gs_m']
コードを変換する
「+ コード」をクリックし, 下記を挿入します.
from opycleid.musicmonoids import PRL_Group _monoid = PRL_Group() print(_monoid.apply_operation('P','C_M')) # C_m print(_monoid.apply_operation('R','C_M')) # A_m print(_monoid.apply_operation('L','C_M')) # E_m print(_monoid.apply_operation('RLRLP','C_M')) # Bb_m
実行すると, 各変換後のコード名が表示されます
['C_m'] ['A_m'] ['E_m'] ['Bb_m']
apply_operation(作用させる変換, コード名)で, 変換後のコード名を取得できます.
使用可能な変換の一覧は下記で表示できます.
for m in PRL_Group().get_morphisms(): print(m[0])
実行結果：
L LP LR LRL LRLP P PL PLP PLRL PR PRL PRP R RL RLP RLR RLRL RLRLP RP RPL RPR RPRL RPRP id_.
注1：結果が同じとなる変換は, 代表する一つの名称のみ定義されています（例：PLPとLPLは同じ結果となるので, PLPのみ定義され, LPLは使用できない）.
注2：id_.は恒等射（自分自身への変換, 何も変換しない）を表します.
コード進行から変換を求める
一つずつコード間の変換を求めるのは面倒なので, コード進行をリストで渡すと, まとめて分析してくれるプログラムを実装してみます.
「+ コード」をクリックし, 下記を挿入します.
from opycleid.musicmonoids import PRL_Group def print_operations(monoid, elms): elm_pairs = list(zip(elms, elms[1:] + elms[:1])) print('-----------------------') for pair in elm_pairs: ops = monoid.get_operation(pair[0], pair[1]) print(f'{pair[0]:4} -> {pair[1]:4} : {"".join(ops):5}') _monoid = PRL_Group() print_operations(_monoid, ['C_M', 'A_m', 'D_m', 'G_M'])
実行すると, いわゆる1625進行の隣接するコード間の変換が全て表示されます（循環進行とみなして, 末尾から先頭への変換も表示します）.
----------------------- C_M -> A_m : R A_m -> D_m : RL D_m -> G_M : PRL G_M -> C_M : LR
コード進行から変換を求める（変換名の置換）
ネオ・リーマン理論では, RPL 以外の特徴的な変換に対して固有の名称が付けられているものがあります.
先ほどのプログラムを少し改造して, 固有の変換名へ置換して表示するようにしてみます.
from opycleid.musicmonoids import PRL_Group def print_operations(monoid, elms): elm_pairs = list(zip(elms, elms[1:] + elms[:1])) print('-----------------------') for pair in elm_pairs: ops = monoid.get_operation(pair[0], pair[1]) print(f'{pair[0]:4} -> {pair[1]:4} : {conv_op("".join(ops)):8}') def conv_op(op): match op: case 'PLP': return 'H' # Hexatonic Pole case 'PRL': return 'F' # Far Fifth case 'RLP': return 'N' # Nebenverwandt (Near Fifth) case 'RPL': return 'S' # Slide case 'RPR': return 'near-T6' # Near T6 case _: return op _monoid = PRL_Group() print_operations(_monoid, ['C_M', 'Gs_m', 'Cs_M', 'Fs_m', 'F_M', 'B_m'])
実行結果：
----------------------- C_M -> Gs_m : H Gs_m -> Cs_M : F Cs_M -> Fs_m : N Fs_m -> F_M : S F_M -> B_m : near-T6 B_m -> C_M : LRL
N（トニック→サブドミナントマイナーを一般化したような変換）や, S（3rdを保持したままルートと5thが半音ズレる）などの変換を表示できるようになります.
注： Opycleid は自分でオリジナルの MonoidAction を定義することができるので, 上記のような細工なしでも自由な名称を付けることが可能です. MonoidAction の定義方法はチュートリアルを参照.
複数のコード進行を比較し, コードを一箇所変えるとどうなるか観察してみると面白いかもしれません.
print_operations(_monoid, ['F_M', 'E_m', 'A_m']) print_operations(_monoid, ['F_M', 'E_M', 'A_m'])
----------------------- F_M -> E_m : LRL E_m -> A_m : RL A_m -> F_M : L ----------------------- F_M -> E_M : PLRL E_M -> A_m : N A_m -> F_M : L
最後に
opycleid.musicmonoids名前空間には他にも, ピッチクラス・セットの移高(Transposition)と転回(Inversion)で三和音を変換する TI_Group_Triadsクラスや, 増三和音を交えた変換に対応する UPL_Monoidクラスなどが用意されています. もちろんオリジナルの変換を定義することも可能です.
ネオ・リーマン理論に興味を持たれた方は, Alexandre Popoff 氏のブログも是非チェックしてみて下さい.
以上
ピッチクラス・セット理論 覚書
このページは無限にサイレント修正されます.
適切に勉強したい方は, 下記の書籍等を当たってください.
The Structure of Atonal Music
Basic Atonal Theory
Introduction to Post-Tonal Theory
Elliott Carter Harmony Book
無調音楽の構造 ピッチクラス・セットの基本的な概念とその考察
ハーモニー探究の歴史 思想としての和声理論 - 第8章 音を秩序づける ポスト調性時代のハーモニー
- 前書き
- ピッチクラス (Pitch class)
- ピッチクラス空間 (Pitch class space)
- 順序付けされたピッチクラス間隔 (Ordered pitch-class interval)
- ピッチクラス・セット (Pitch-class sets)
- 基数 (Cardinal Number)
- Mod 12
- 移置 (Transposition)
- 転回 (Inversion)
- TnI
- Multiplication
- M
- MI
- 正規の順序 (Normal order)
- 原型 (Prime form)
- Forte number
- インターバルクラス (Interval class)
- Interval vector
- Z-relation
- Complement
- サブセット (Subset)
- スーパーセット (Superset)
- Common-tone theorem
- Hexachord theorem
- All-interval tetrachord
- All-trichord hexachord
前書き
ピッチクラス・セット理論 ( Musical set theory ) は, 文献や音楽理論家ごとに使用する用語・記号等が異なります. 下記は代表的な音楽理論家, 及びその主著
- Allen Forte - The Structure of Atonal Music (1973)
- John Rahn - Basic Atonal Theory (1980)
以下, 単にForte, Rahnと書いた場合は, 上記を示します.
ピッチクラス (Pitch class)
同じ音名を与えられている, nオクターブ離れた音の集合(nは整数).
0〜11の整数で表記する (Integer notation).
10と11は, AとBで表記する場合がある.
| 音名 | ピッチクラス |
|---|---|
| C | 0 |
| C♯/D♭ | 1 |
| D | 2 |
| D♯/E♭ | 3 |
| E | 4 |
| F | 5 |
| F♯/G♭ | 6 |
| G | 7 |
| G♯/A♭ | 8 |
| A | 9 |
| A♯/B♭ | 10 or A |
| B | 11 or B |
ピッチクラス空間 (Pitch class space)
ピッチクラスの関係をモデル化したもの. ピッチクラスを 0, 1, ... 10, 11 と円型に並べて表す. 11の次は, また始点の0へと戻る.
順序付けされたピッチクラス間隔 (Ordered pitch-class interval)
2つのピッチクラス間の, 順序を考慮した間隔.
- 例：11から見て7への間隔は+8
→ → 11 0 1 2 3 4 5 6 7
- 例：2から見て10への間隔は-4
← ← 10 11 0 1 2
ピッチクラス・セット (Pitch-class sets)
ピッチクラスで構成される集まり（以下, PCセット ）. 重複するピッチクラスは除かれる.
- 例：Cメジャーコード
| 構成音 | PCセット |
|---|---|
| C E G | [0, 4, 7] |
- 例：ダイアトニックスケール
| 構成音 | PCセット |
|---|---|
| C D E F G A B | [0, 2, 4, 5, 7, 9, B] |
基数 (Cardinal Number)
PCセットに含まれるピッチクラスの個数.
- 例：[0, 1, 2, 3] → 基数は4
- 例：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B] → 基数は12
Mod 12
整数 aとbについて, それぞれをnで割った余りが等しいことを
a ≡ b (mod n)
と表記する（合同式）.
ピッチクラス空間は 0 〜 11 の中で閉じているため, mod 12 の合同式として計算が行われる.
移置 (Transposition)
PCセット内の全てのピッチクラスに, 任意の整数を加算する操作.
整数nを加算することを Tn と表記する.
- 例：[0, 1, 2]のT11
0 + 11 = 11 1 + 11 = 12 ≡ 0 (mod 12) 2 + 11 = 13 ≡ 1 (mod 12) より → [B, 0, 1]
- 例：[0, 1, 2] の T0 〜 T11
| Tn | PCセット |
|---|---|
| T0 | [0, 1, 2] |
| T1 | [1, 2, 3] |
| T2 | [2, 3, 4] |
| T3 | [3, 4, 5] |
| T4 | [4, 5, 6] |
| T5 | [5, 6, 7] |
| T6 | [6, 7, 8] |
| T7 | [7, 8, 9] |
| T8 | [8, 9, A] |
| T9 | [9, A, B] |
| T10 | [A, B, 0] |
| T11 | [B, 0, 1] |
転回 (Inversion)
PCセット内の全てのピッチクラスを, 指定した対称軸で反転させる操作.
0-6を結ぶ線を対称軸として転回することを I と表記する.
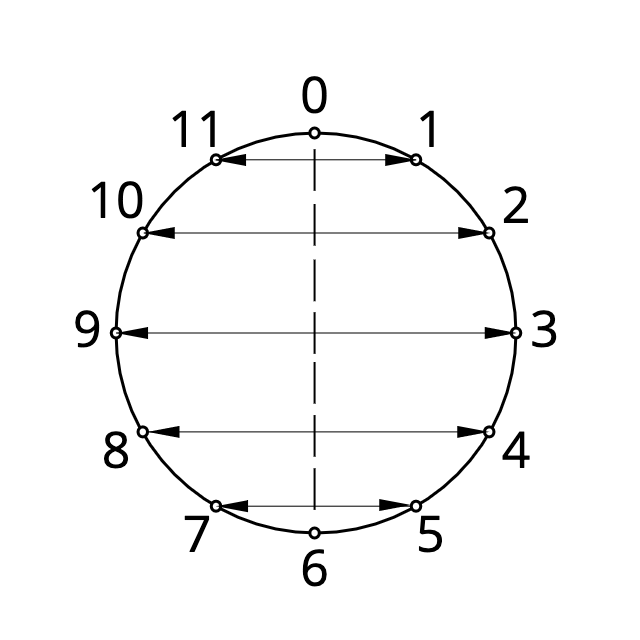
- 例：[0, 1, 4, 6]の I
0 → 0 1 → 11 4 → 8 6 → 6 より → [0,B,8,6]
対称軸は12種類あり, それぞれの対称軸による転回を I0 〜 I11 と表記する.
| 対象軸 | In |
|---|---|
| 0 - 6 | I0 |
| 0,1 - 6,7 | I1 |
| 1 - 7 | I2 |
| 1,2 - 7,8 | I3 |
| 2 - 8 | I4 |
| 2,3 - 8,9 | I5 |
| 3 - 9 | I6 |
| 3,4 - 9,10 | I7 |
| 4 - 10 | I8 |
| 4,5 - 10,11 | I9 |
| 5 - 11 | I10 |
| 5,6 - 11,0 | I11 |
TnI
転回(Inversion) と 移置(Transposition) の合成.
転回(I) したあと, nだけ 移置(Tn) する操作.
また, In と TnI は同値.
Multiplication
PCセットに含まれる全てのピッチクラスを, 指定した値で乗算(mod 12)する操作. *1
n を乗算する操作を Mn と表記する.
- 例：[0, 1, 4, 6] の M5
0 × 5 = 0 1 × 5 = 5 4 × 5 = 20 ≡ 8 (mod 12) 6 × 5 = 30 ≡ 6 (mod 12) → [0,5,6,8]
また, M11 と I は同値.
M
M5を単に M と表記する.
MI
転回(Inversion) と Multiplication 5(M5) の合成.
転回(I) したあと5を乗算する(M)操作を表す.
また, MI と M7 は同値.
I, M, MI の関係を図示すると,
- m2 - 短2度圏
- P4 - 完全4度圏
- P5 - 完全5度圏
- M7 - 長7度圏
の変換と捉えることができる.
正規の順序 (Normal order)
もしくは Normal form.
PCセットを並び替えて, 最も"コンパクト"になる場合の順序.
正規の順序, 原型(後述)を求めるアルゴリズムは Forte と Rahn で異なる.
どちらのアルゴリズムもほぼ同一の結果となるが, 一部のPCセットでは原型が異なる.
(これはアルゴリズムに誤りがあるというわけではなく, "コンパクト"の解釈の違いによるもの)
正規の順序の求め方 パターン1：間隔の比較が1回で完了する場合
例 [0,1,9,8] 1. PCセットを昇順に並べ替える [0,1,9,8] → [0,1,8,9] 2. 全てのローテーションを列挙する(基数4なので4種類) a. [0,1,8,9] b. [1,8,9,0] c. [8,9,0,1] d. [9,0,1,8] 3. 最左と最右の間隔を求める a. 9 - 0 = 9 b. 0 - 1 = -1 ≡ 11 (mod 12) c. 1 - 8 = -7 ≡ 5 (mod 12) d. 8 - 9 = -1 ≡ 11 (mod 12) 4. 間隔が最小になる(最もコンパクト)なものが, 正規の順序 → c. [8,9,0,1]
正規の順序の求め方 パターン2：間隔の比較が2回以上必要な場合
例 [0,5,1,8] 1. PCセットを昇順に並べ替える [0,5,1,8] → [0,1,5,8] 2. 全てのローテーションを列挙する a. [0,1,5,8] b. [1,5,8,0] c. [5,8,0,1] d. [8,0,1,5] 3. 最左と最右の間隔を求める a. 8 - 0 = 8 b. 0 - 1 = -1 ≡ 11 ( mod 12 ) c. 1 - 5 = -4 ≡ 8 ( mod 12 ) d. 5 - 8 = -3 ≡ 9 ( mod 12 ) 4. 間隔が最小になるものが2つあるため比較を続ける ここから Forte と Rahn でアルゴリズムが異なる a. [0,1,5,8] c. [5,8,0,1]
[ Forte のアルゴリズム]
5. 最左と「最左から2番目」の間隔を比較する
a. 1 - 0 = 1
c. 8 - 5 = 3
6. 比較の結果, 間隔が最小のものが複数ある場合は
最左と「最左から3番目」を比較
最左と「最左から4番目」を比較
：
と間隔が最小のものが1つになるまで繰り返す
7. 間隔の比較が最小になるものが, 正規の順序
→ a. [0,1,5,8]
[ Rahn のアルゴリズム]
5'. 最左と「最右から2番目」の間隔を比較する
a. 5 - 0 = 5
c. 0 - 5 = -5 ≡ 7 ( mod 12 )
6'. 比較の結果, 間隔が最小のものが複数ある場合は
最左と「最右から3番目」を比較
最左と「最右から4番目」を比較
：
と間隔が最小のものが1つになるまで繰り返す
7'. 間隔の比較が最小になるものが, 正規の順序
→ a. [0,1,5,8]
正規の順序の求め方 パターン3：間隔の比較で決定できない場合
例 [0, 8, 4] 1. PCセットを昇順に並べ替える [0,8,4] → [0,4,8] 2. 全てのローテーションを列挙する a. [0,4,8] b. [4,8,0] c. [8,0,4] 3. 最左と最右の間隔を求める a. 8 - 0 = 8 b. 0 - 4 = -4 ≡ 8 ( mod 12 ) c. 4 - 8 = -4 ≡ 8 ( mod 12 ) 4. 間隔が最小になるものが3つあるため比較を続ける （基数3で Forte, Rahn どちらのアルゴリズムも 計算過程が一致するため, 以降はまとめて記述） 5. 最左と「最左(最右)から2番目」の間隔を比較する a. 4 - 0 = 4 b. 8 - 4 = 4 c. 0 - 8 = -8 ≡ 4 ( mod 12 ) 6. 全ての間隔を比較しても, 間隔が最小のものを1つに絞り込めない場合は, 最小ピッチクラスから始まるものを正規の順序とする → a. [0,4,8]
補足：Forte と Rahn のアルゴリズムで原型が異なるPCセットの一覧
| Forte number | Forte の場合 | Rahn の場合 |
|---|---|---|
| 5-20 | [0, 1, 3, 7, 8] | [0,1,5,6,8] |
| 6-Z29 | [0, 1, 3, 6, 8, 9] | [0, 2, 3, 6, 7, 9] |
| 6-31 | [0, 1, 3, 5, 8, 9] | [0, 1, 4, 5, 7, 9] |
| 7-Z18 | [0, 1, 4, 5, 6, 7, 9] | [0, 2, 3, 4, 5, 8, 9] |
| 7-20 | [0, 1, 2, 5, 6, 7, 9] | [0, 1, 2, 4, 7, 8, 9] |
| 8-26 | [0, 1, 3, 4, 5, 7, 8, A] | [0, 1, 2, 4, 5, 7, 9, A] |
原型 (Prime form)
任意のPCセットは移置Tnと転回Iの操作によって24種類に変換される. この中で最も"標準的"な1種類を代表のPCセットとして選び, 24種類全体の識別子として用いる. これを 原型(Prime form) と呼ぶ.
- 例：[0, 1, 2, 6]をTnとIで変形
| No. | 操作 | PCセット(正規の順序) |
|---|---|---|
| 1 | T0 | [0, 1, 2, 6] |
| 2 | T1 | [1, 2, 3, 7] |
| 3 | T2 | [2, 3, 4, 8] |
| 4 | T3 | [3, 4, 5, 9] |
| 5 | T4 | [4, 5, 6, A] |
| 6 | T5 | [5, 6, 7, B] |
| 7 | T6 | [6, 7, 8, 0] |
| 8 | T7 | [7, 8, 9, 1] |
| 9 | T8 | [8, 9, A, 2] |
| 10 | T9 | [9, A, B, 3] |
| 11 | T10 | [A, B, 0, 4] |
| 12 | T11 | [B, 0, 1, 5] |
| 13 | T0I | [6, A, B, 0] |
| 14 | T1I | [7, B, 0, 1] |
| 15 | T2I | [8, 0, 1, 2] |
| 16 | T3I | [9, 1, 2, 3] |
| 17 | T4I | [A, 2, 3, 4] |
| 18 | T5I | [B, 3, 4, 5] |
| 19 | T6I | [0, 4, 5, 6] |
| 20 | T7I | [1, 5, 6, 7] |
| 21 | T8I | [2, 6, 7, 8] |
| 22 | T9I | [3, 7, 8, 9] |
| 23 | T10I | [4, 8, 9, A] |
| 24 | T11I | [5, 9, A, B] |
- 原型の求め方 例：[1,8,7,9]
1. 正規の順序 ( Normal order ) を求める [1,8,7,9] → [7,8,9,1] 2. 0から始まるように移置 ( Transposition ) する [7,8,9,1]をT_5で移置 → [0,1,2,6] 3. 元のPCセットを転回し, 1,2の手順を繰り返す [1,8,7,9]をIで転回 → [B,4,5,3] [B,4,5,3]を正規の順序へ → [B,3,4,5] [B,3,4,5]をT_1で移置 → [0,4,5,6] 4. 2と3で求めたPCセットを比較して, より左に詰められている ( packed ) 方が原型 0 1 2 _ _ _ 6 _ _ _ _ _ ← 左詰め 0 _ _ _ 4 5 6 _ _ _ _ _ → [0,1,2,6]が原型
Forte number
原型に名称を割当てる方法の一種で, 「(基数) - (連番)」の形で表記される.
- 例：
[0,1,3,5,6,8,A] → 7-35
また, Z-relation (後述)を持つ原型は, 「(基数) - Z(連番)」の形で表記される.
- 例：
[0,1,4,6] → 4-Z15
全ての原型と Forte number のリストは下記を参照.
List of pitch-class sets(Wikipedia)
A Brief Introduction to Pitch-Class Set Analysis : Table of pc set classes
Forte numberの決定方法
Forte number は下記の手順で決定される 1. 原型を基数ごとのグループに分類する. 2. 各グループ内を「Interval vectorの降順」 で並び替える. 3. Z-relationの対を持つ原型は, より「左詰め」の方をそのままの位置に, 他方をリストの最後尾へ移動する.
例：基数4の原型の順序 4-1 [0,1,2,3] <321000> 4-2 [0,1,2,4] <221100> 4-3 [0,1,3,4] <212100> 4-4 [0,1,2,5] <211110> 4-5 [0,1,2,6] <210111> 4-6 [0,1,2,7] <210021> 4-7 [0,1,4,5] <201210> 4-8 [0,1,5,6] <200121> 4-9 [0,1,6,7] <200022> 4-10 [0,2,3,5] <122010> 4-11 [0,1,3,5] <121110> 4-12 [0,2,3,6] <112101> 4-13 [0,1,3,6] <112011> 4-14 [0,2,3,7] <111120> 4-Z15 [0,1,4,6] <111111> ← そのままの位置 4-16 [0,1,5,7] <110121> 4-17 [0,3,4,7] <102210> 4-18 [0,1,4,7] <102111> 4-19 [0,1,4,8] <101310> 4-20 [0,1,5,8] <101220> 4-21 [0,2,4,6] <030201> 4-22 [0,2,4,7] <021120> 4-23 [0,2,5,7] <021030> 4-24 [0,2,4,8] <020301> 4-25 [0,2,6,8] <020202> 4-26 [0,3,5,8] <012120> 4-27 [0,2,5,8] <012111> 4-28 [0,3,6,9] <004002> 4-Z29 [0,1,3,7] <111111> ← 最後尾へ移動
補足：PCセットの計算ツール
| リンク | 説明 |
|---|---|
| Pitch Class Set Calculator | Androidアプリ. 設定で Forte, Rahn のアルゴリズムを切替可能. |
| Music Calculators | Jeremiah Goyette氏のWebサイト. 非常に多機能かつ高機能な各種計算ツール. |
インターバルクラス (Interval class)
順序付けされないピッチクラス間隔 (Unordered pitch-class interval) はインターバルクラスと呼ばれる.
0 ~ 11を円形に並べたとき,
2つのピッチクラスの「右回りの間隔」と「左回りの間隔」を比較し, 小さい方をインターバルクラスとする.
- 例：0と5のピッチクラス間隔は右回りの方が小さいので, インターバルクラス = 5
| インターバルクラス | 対応するピッチクラス間隔 |
|---|---|
| 1 | 1 and 11 |
| 2 | 2 and 10 |
| 3 | 3 and 9 |
| 4 | 4 and 8 |
| 5 | 5 and 7 |
| 6 | 6 |
Interval vector
もしくは Interval-class vector.
PCセットに含まれる全てのインターバルクラス1 ~ 6について, それぞれの個数を数え上げ列挙したもの. *2
- 例：[0,1,3,5,6,8,A]
1. PCセットに含まれる全てのインターバルクラスを列挙.
0と1の間 → 1
0と3の間 → 3
：
6とAの間 → 4
8とAの間 → 2
0 1 3 5 6 8 A
-------------
1 2 2 1 2 2
3 4 3 3 4
5 5 5 5
6 5 5
4 3
2
2. インターバルクラス(ic)1 ~ 6の個数を数え上げる.
ic1 × 2
ic2 × 5
ic3 × 4
ic4 × 3
ic5 × 6
ic6 × 1
3. 左からic1 ~ ic6の順に並べる.
⟨254361⟩
Z-relation
Interval vector が同一のPCセットが, 転回関係にも移置関係にもないとき, この関係を Z-relation と呼ぶ.
- 例：4-Z15 と 4-Z29 は Z-relation
| Forte number | 原型 | Interval vector |
|---|---|---|
| 4-Z15 | [0, 1, 4, 6] | <111111> |
| 4-Z29 | [0, 1, 3, 7] | <111111> |
12平均律のPCセットにおいて Z-relation は常に対 ( pair ) で現れるが, より大きい平均律(16EDOなど)では3つ組以上の Z-relation があることが知られている.
Complement
あるPCセット X に含まれない全てのピッチクラスで構成されたPCセット Y があるとき, Y は X の Complement である.
- 例：
[0,1,2,3,4,5,6,7]の Complement は[8,9,A,B]である
サブセット (Subset)
あるPCセット X, Y に関して, X が Y に包括されるとき, X は Y のサブセットである.
- 例：
[0,1,2]は[0,1,2,5]のサブセットである
スーパーセット (Superset)
あるPCセット X, Y に関して, X が Y に包括されるとき, Y は X のスーパーセットである.
- 例：
[0,1,2,5]は[0,1,2]のスーパーセットである
Common-tone theorem
あるPCセット X の Interval vector と, X をnだけ移置したPCセット Tn(X) と X の共通音(共通ピッチクラス )の関係を表す定理.
PCセット X の Interval vector が<ic1 ic2 ic3 ic4 ic5 ic6>のとき, X と Tn(X) の共通音の個数との関係は
| X と Tn(X) | 共通音の個数 |
|---|---|
| X と T1(X) | ic1 個 |
| X と T2(X) | ic2 個 |
| X と T3(X) | ic3 個 |
| X と T4(X) | ic4 個 |
| X と T5(X) | ic5 個 |
| X と T6(X) | ic6 × 2 個 |
| X と T7(X) | ic5 個 |
| X と T8(X) | ic4 個 |
| X と T9(X) | ic3 個 |
| X と T10(X) | ic2 個 |
| X と T11(X) | ic1 個 |
直感的には, Interval vector は和音を平行移動したときの共通音の個数を表している, と捉えることができる.
- 例：Cメジャースケールを平行移動(転調)した場合の共通音
Cメジャースケール [0, 2, 4, 5, 7, 9, B] <254361>
| Key | PCセット | Key Cとの共通音数 |
|---|---|---|
| C♯/D♭ | [1, 3, 5, 6, 8, A, 0] | 2個 |
| D | [2, 4, 6, 7, 9, B, 1] | 5個 |
| D♯/E♭ | [3, 5, 7, 8, A, 0, 2] | 4個 |
| E | [4, 6, 8, 9, B, 1, 3] | 3個 |
| F | [5, 7, 9, A, 0, 2, 4] | 6個 |
| F♯/G♭ | [6, 8, A, B, 1, 3, 5] | 2個 |
| G | [7, 9, B, 0, 2, 4, 6] | 6個 |
| G♯/A♭ | [8, A, 0, 1, 3, 5, 7] | 3個 |
| A | [9, B, 1, 2, 4, 6, 8] | 4個 |
| A♯/B♭ | [A, 0, 2, 3, 5, 7, 9] | 5個 |
| B | [B, 1, 3, 4, 6, 8, A] | 2個 |
ダイアトニックスケール(7-35)にインターバルクラス1は2個含まれるので, インターバルクラス1の移置である T1 (半音上に転調)と T11 (半音下に転調)の場合, 共通音数が2個であることが読み取れる.
いわゆる関係調であるF,Gは共通音が多く(6個), 一方で遠隔調であるC♯,F♯,Bは共通音が少ない(2個)ことが読み取れる.
Hexachord theorem
12平均律において, 基数6のPCセット A とその Complement の Ac が異なる原型になるとき, A と Ac は Z-relation である.
例：
6-Z6 [0,1,2,5,6,7]の Complement を原型にすると6-Z38 [0,1,2,3,7,8]→ Z-relation である例：
6-1 [0,1,2,3,4,5]の Complement を原型にすると6-1 [0,1,2,3,4,5]→ 異なる原型ではない
All-interval tetrachord
全てのインターバルクラス1 ~ 6を1つずつ含む最小基数のPCセット.
全ての音程(interval)を内包する四和音(tetrachord)の意.
下記の2種類で, それらは Z-relation である.
4-Z15 [0,1,4,6] <111111>4-Z29 [0,1,3,7] <111111>
All-trichord hexachord
基数3の全てのPCセットの原型12種類(3-1 ~ 3-12)をサブセットとして内包する最小基数のPCセット.
全ての三和音(trichord)を内包する六和音(hexachord)の意.
下記の1種類.
6-Z17 [0,1,2,4,7,8] <322332>
*1: ピエール・ブーレーズがLe Marteau sans maîtreで用いた "Pitch multiplication" とは異なる.
